 login/create account
login/create account
tree
A gold-grabbing game ★★
Author(s): Rosenfeld
Setup Fix a tree  and for every vertex
and for every vertex 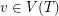 a non-negative integer
a non-negative integer 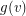 which we think of as the amount of gold at
which we think of as the amount of gold at  .
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex  of the tree, takes the gold at this vertex, and then deletes
of the tree, takes the gold at this vertex, and then deletes  . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
. The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Problem Find optimal strategies for the players.
Graphs with a forbidden induced tree are chi-bounded ★★★
Author(s): Gyarfas
Say that a family 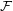 of graphs is
of graphs is 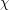 -bounded if there exists a function
-bounded if there exists a function 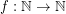 so that every
so that every 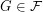 satisfies
satisfies 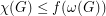 .
.
Conjecture For every fixed tree  , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to  is
is 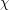 -bounded.
-bounded.
 , the family of graphs with no induced subgraph isomorphic to
, the family of graphs with no induced subgraph isomorphic to  is
is 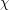 -bounded.
-bounded. Keywords: chi-bounded; coloring; excluded subgraph; tree
Does the chromatic symmetric function distinguish between trees? ★★
Author(s): Stanley
Problem Do there exist non-isomorphic trees which have the same chromatic symmetric function?
Keywords: chromatic polynomial; symmetric function; tree
Graham's conjecture on tree reconstruction ★★
Author(s): Graham
Problem for every graph  , we let
, we let 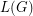 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 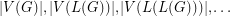 ?
?
 , we let
, we let 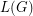 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 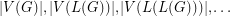 ?
? Keywords: reconstruction; tree

 Drupal
Drupal CSI of Charles University
CSI of Charles University