login/create account
game
Transversal achievement game on a square grid ★★
Author(s): Erickson
Problem Two players alternately write O's (first player) and X's (second player) in the unoccupied cells of an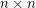 
grid. The first player (if any) to occupy a set of 
cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
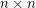grid. The first player (if any) to occupy a set of cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play? Keywords: game
Square achievement game on an n x n grid ★★
Author(s): Erickson
Problem Two players alternately write O's (first player) and X's (second player) in the unoccupied cells of an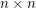 
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
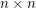grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15. Keywords: game
A gold-grabbing game ★★
Author(s): Rosenfeld
Setup Fix a tree 
and for every vertex 
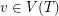a non-negative integer 
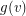which we think of as the amount of gold at 
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex of the tree, takes the gold at this vertex, and then deletes . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Problem Find optimal strategies for the players.
Drupal
CSI of Charles University