 login/create account
login/create account
A gold-grabbing game
Setup Fix a tree  and for every vertex
and for every vertex 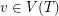 a non-negative integer
a non-negative integer 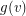 which we think of as the amount of gold at
which we think of as the amount of gold at  .
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex  of the tree, takes the gold at this vertex, and then deletes
of the tree, takes the gold at this vertex, and then deletes  . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
. The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Problem Find optimal strategies for the players.
In the special case when  is a path of even length, the first player can ensure that she chooses either all of the even vertices, or all of the odd vertices. Thus, player 1 should never finish with less than player 2, and whenever the total gold on the odd vertices and the total gold on the even vertices are not equal, there is a winning strategy for player 1.
is a path of even length, the first player can ensure that she chooses either all of the even vertices, or all of the odd vertices. Thus, player 1 should never finish with less than player 2, and whenever the total gold on the odd vertices and the total gold on the even vertices are not equal, there is a winning strategy for player 1.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Not an open problem in the strict sense
There exists an obvious algorithm which just enumerates all variants.
The problem seems to mean to find a more efficient algorithm. This is not a strict formulation because it is not strictly defined what is "more efficient".
I suggest to rip this problem, such as to put it into Second tier problems.
--
Victor Porton - http://www.mathematics21.org