login/create account
Setup Fix a tree 
and for every vertex 
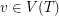a non-negative integer 
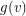which we think of as the amount of gold at 
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex of the tree, takes the gold at this vertex, and then deletes . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Problem Find optimal strategies for the players.
In the special case when is a path of even length, the first player can ensure that she chooses either all of the even vertices, or all of the odd vertices. Thus, player 1 should never finish with less than player 2, and whenever the total gold on the odd vertices and the total gold on the even vertices are not equal, there is a winning strategy for player 1.
Bibliography
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University