Open Problem Garden

Importance: High ✭✭✭

Author(s):

Subject:	Combinatorics
	» Matrices

Keywords:	invertible
	nowhere-zero flow

Recomm. for undergrads: no

Prize: none

Posted	by:	mdevos
	on:	March 8th, 2007

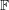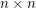Conjecture If ${\mathbb F}$ is a finite field with at least 4 elements and $A$ is an invertible $n \times n$ matrix with entries in 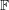${\mathbb F}$ , then there are column vectors 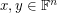$x,y \in {\mathbb F}^n$ which have no coordinates equal to zero such that $Ax=y$ .

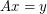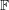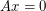The motivation for this problem comes from the study of nowhere-zero flows on graphs. If $A$ is the directed incidence matrix of a graph $G$ , then a nowhere-zero ${\mathbb F}$ -flow on $G$ is precisely a vector $x$ so that $x$ has all entries nonzero, and $Ax=0$ . The above conjecture is similar, but is for general (invertible) matrices. Alon and Tarsi have resolved this conjecture for all fields not of prime order using their polynomial technique.

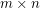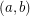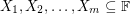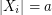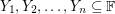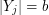Definition: Say that a $m \times n$ matrix $A$ is $(a,b)$ -choosable if for all $X_1,X_2,\ldots,X_m \subseteq {\mathbb F}$ with $|X_i|=a$ and for all $Y_1,Y_2,\ldots,Y_n \subseteq {\mathbb F}$ with $|Y_j|=b$ , there exists a vector 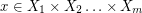$x \in X_1 \times X_2 \ldots \times X_m$ and a vector 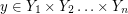$y \in Y_1 \times Y_2 \ldots \times Y_n$ so that 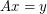$Ax=y$ . Note that every matrix is 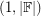$(1,|{\mathbb F}|)$ -choosable, but that an 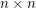$n \times n$ matrix is 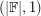$(|{\mathbb F}|,1)$ -choosable if and only if it is invertible.

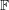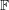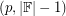Alon and Tarsi actually prove a stronger property than Jaeger conjectured for fields not of prime order. They prove that if ${\mathbb F}$ has characteristic $p$ , then every invertible matrix over ${\mathbb F}$ is $(p,|{\mathbb F}|-1)$ -choosable. This result has been extended by DeVos [D] who showed that every such matrix is 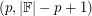$(p,|{\mathbb F}|-p+1)$ -choosable. Yang Yu [Y] has verified that the conjecture holds for 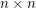$n \times n$ matrices with entries in 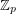${\mathbb Z}_p$ when $n < 2^{p-2}$ .

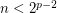Jaeger's conjecture is true in a very strong sense for fields of characteristic 2. DeVos [D] proved that every invertible matrix over such a field is 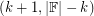$(k+1,|{\mathbb F}|-k)$ -choosable for every $k$ . The following conjecture asserts that invertible matrices over fields of prime order have choosability properties nearly as strong.

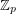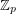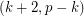Conjecture [The choosability in ${\mathbb Z}_p$ conjecture (DeVos)] Every invertible matrix with entries in ${\mathbb Z}_p$ for a prime $p$ is $(k+2,p-k)$ -choosable for every $k$ .

This is essentially the strongest choosability conjecture one might hope to be true over fields of prime order. I (M. DeVos) don't have any experimental evidence for this at all, so it could be false already for some small examples. However, I suspect that if The permanent conjecture is true, that this conjecture should also be true. In any case, I (M. DeVos) am offering a bottle of wine for this conjecture.

Bibliography

[A] N. Alon, Combinatorial Nullstellensatz, Combinatorics Probability and Computing 8 (1999) no. 1-2, 7-29. MathSciNet

[AT] N. Alon, M. Tarsi, A Nowhere-Zero Point in Linear Mappings, Combinatorica 9 (1989), 393-395. MathSciNet

[BBLS] R. Baker, J. Bonin, F. Lazebnik, and E. Shustin, On the number of nowhere-zero points in linear mappings, Combinatorica 14 (2) (1994), 149-157. MathSciNet

[D] M. DeVos, Matrix Choosability, J. Combinatorial Theory, Ser. A 90 (2000), 197-209. MathSciNet

[Y] Y. Yu, The Permanent Rank of a Matrix, J. Combinatorial Theory Ser. A 85 (1999), 237-242. MathSciNet

* indicates original appearance(s) of problem.

add new comment

Open Problem Garden

Bibliography

Reply

Navigate

Recent Activity