 login/create account
login/create account
A nowhere-zero point in a linear mapping
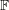 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 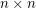 matrix with entries in
matrix with entries in 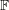 , then there are column vectors
, then there are column vectors 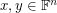 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 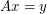 .
. The motivation for this problem comes from the study of nowhere-zero flows on graphs. If  is the directed incidence matrix of a graph
is the directed incidence matrix of a graph  , then a nowhere-zero
, then a nowhere-zero 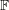 -flow on
-flow on  is precisely a vector
is precisely a vector  so that
so that  has all entries nonzero, and
has all entries nonzero, and 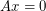 . The above conjecture is similar, but is for general (invertible) matrices. Alon and Tarsi have resolved this conjecture for all fields not of prime order using their polynomial technique.
. The above conjecture is similar, but is for general (invertible) matrices. Alon and Tarsi have resolved this conjecture for all fields not of prime order using their polynomial technique.
Definition: Say that a 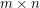 matrix
matrix  is
is 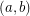 -choosable if for all
-choosable if for all 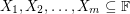 with
with 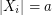 and for all
and for all 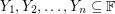 with
with 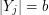 , there exists a vector
, there exists a vector 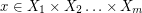 and a vector
and a vector 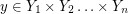 so that
so that 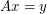 . Note that every matrix is
. Note that every matrix is 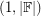 -choosable, but that an
-choosable, but that an 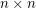 matrix is
matrix is 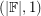 -choosable if and only if it is invertible.
-choosable if and only if it is invertible.
Alon and Tarsi actually prove a stronger property than Jaeger conjectured for fields not of prime order. They prove that if 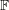 has characteristic
has characteristic  , then every invertible matrix over
, then every invertible matrix over 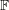 is
is 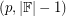 -choosable. This result has been extended by DeVos [D] who showed that every such matrix is
-choosable. This result has been extended by DeVos [D] who showed that every such matrix is 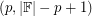 -choosable. Yang Yu [Y] has verified that the conjecture holds for
-choosable. Yang Yu [Y] has verified that the conjecture holds for 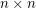 matrices with entries in
matrices with entries in 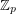 when
when 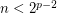 .
.
Jaeger's conjecture is true in a very strong sense for fields of characteristic 2. DeVos [D] proved that every invertible matrix over such a field is 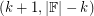 -choosable for every
-choosable for every  . The following conjecture asserts that invertible matrices over fields of prime order have choosability properties nearly as strong.
. The following conjecture asserts that invertible matrices over fields of prime order have choosability properties nearly as strong.
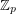 conjecture (DeVos)] Every invertible matrix with entries in
conjecture (DeVos)] Every invertible matrix with entries in 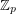 for a prime
for a prime  is
is 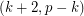 -choosable for every
-choosable for every  .
. This is essentially the strongest choosability conjecture one might hope to be true over fields of prime order. I (M. DeVos) don't have any experimental evidence for this at all, so it could be false already for some small examples. However, I suspect that if The permanent conjecture is true, that this conjecture should also be true. In any case, I (M. DeVos) am offering a bottle of wine for this conjecture.
Bibliography
[A] N. Alon, Combinatorial Nullstellensatz, Combinatorics Probability and Computing 8 (1999) no. 1-2, 7-29. MathSciNet
[AT] N. Alon, M. Tarsi, A Nowhere-Zero Point in Linear Mappings, Combinatorica 9 (1989), 393-395. MathSciNet
[BBLS] R. Baker, J. Bonin, F. Lazebnik, and E. Shustin, On the number of nowhere-zero points in linear mappings, Combinatorica 14 (2) (1994), 149-157. MathSciNet
[D] M. DeVos, Matrix Choosability, J. Combinatorial Theory, Ser. A 90 (2000), 197-209. MathSciNet
[Y] Y. Yu, The Permanent Rank of a Matrix, J. Combinatorial Theory Ser. A 85 (1999), 237-242. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University