 login/create account
login/create account
Search
Results 21-40 of 43
Mixing Circular Colourings ★
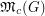 always rational?
always rational? Keywords: discrete homotopy; graph colourings; mixing
What is the homotopy type of the group of diffeomorphisms of the 4-sphere? ★★★★
Author(s): Smale
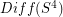 has the homotopy-type of a product space
has the homotopy-type of a product space 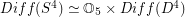 where
where 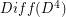 is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of
is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of 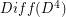 .
. Keywords: 4-sphere; diffeomorphisms
Blatter-Specker Theorem for ternary relations ★★
Author(s): Makowsky
Let  be a class of finite relational structures. We denote by
be a class of finite relational structures. We denote by 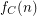 the number of structures in
the number of structures in  over the labeled set
over the labeled set 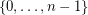 . For any class
. For any class  definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every
definable in monadic second-order logic with unary and binary relation symbols, Specker and Blatter showed that, for every 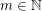 , the function
, the function 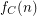 is ultimately periodic modulo
is ultimately periodic modulo  .
.
Keywords: Blatter-Specker Theorem; FMT00-Luminy
Shuffle-Exchange Conjecture ★★★
Author(s): Beneš; Folklore; Stone
Given integers 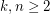 , let
, let 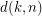 be the smallest integer
be the smallest integer 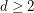 such that the symmetric group
such that the symmetric group 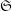 on the set of all words of length
on the set of all words of length  over a
over a  -letter alphabet can be generated as
-letter alphabet can be generated as 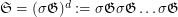 (
( times), where
times), where 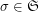 is the shuffle permutation defined by
is the shuffle permutation defined by 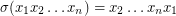 , and
, and 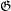 is the exchange group consisting of all permutations in
is the exchange group consisting of all permutations in 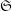 preserving the first
preserving the first 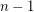 letters in the words.
letters in the words.
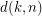 .
. 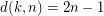 , for all
, for all 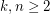 .
. Keywords:
Refuting random 3SAT-instances on $O(n)$ clauses (weak form) ★★★
Author(s): Feige
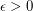 and every rational
and every rational 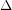 , there is no polynomial-time algorithm for the following problem.
, there is no polynomial-time algorithm for the following problem.
Given is a 3SAT (3CNF) formula 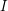 on
on  variables, for some
variables, for some  , and
, and 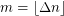 clauses drawn uniformly at random from the set of formulas on
clauses drawn uniformly at random from the set of formulas on  variables. Return with probability at least 0.5 (over the instances) that
variables. Return with probability at least 0.5 (over the instances) that 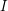 is typical without returning typical for any instance with at least
is typical without returning typical for any instance with at least 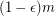 simultaneously satisfiable clauses.
simultaneously satisfiable clauses.
Keywords: NP; randomness in TCS; satisfiability
Ohba's Conjecture ★★
Author(s): Ohba
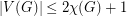 , then
, then 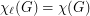 .
. Keywords: choosability; chromatic number; complete multipartite graph; list coloring
Beneš Conjecture (graph-theoretic form) ★★★
Author(s): Beneš
 ) Find a sufficient condition for a straight
) Find a sufficient condition for a straight 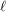 -stage graph to be rearrangeable. In particular, what about a straight uniform graph?
-stage graph to be rearrangeable. In particular, what about a straight uniform graph?  ) Let
) Let 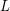 be a simple regular ordered
be a simple regular ordered  -stage graph. Suppose that the graph
-stage graph. Suppose that the graph 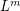 is externally connected, for some
is externally connected, for some 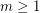 . Then the graph
. Then the graph 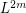 is rearrangeable.
is rearrangeable. Keywords:
Beneš Conjecture ★★★
Author(s): Beneš
Let  be a non-empty finite set. Given a partition
be a non-empty finite set. Given a partition 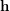 of
of  , the stabilizer of
, the stabilizer of 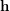 , denoted
, denoted 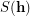 , is the group formed by all permutations of
, is the group formed by all permutations of  preserving each block of
preserving each block of 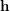 .
.
 ) Find a sufficient condition for a sequence of partitions
) Find a sufficient condition for a sequence of partitions 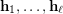 of
of  to be complete, i.e. such that the product of their stabilizers
to be complete, i.e. such that the product of their stabilizers 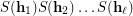 is equal to the whole symmetric group
is equal to the whole symmetric group 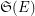 on
on  . In particular, what about completeness of the sequence
. In particular, what about completeness of the sequence 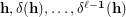 , given a partition
, given a partition 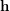 of
of  and a permutation
and a permutation  of
of  ?
? 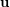 be a uniform partition of
be a uniform partition of  and
and 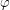 be a permutation of
be a permutation of  such that
such that 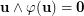 . Suppose that the set
. Suppose that the set 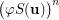 is transitive, for some integer
is transitive, for some integer 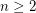 . Then
. Then 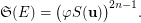
Keywords:
Inward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; inward reloid; reloid
Distributivity of union of funcoids corresponding to reloids ★★
Author(s): Porton
Keywords: funcoid; infinite distributivity; reloid
Square achievement game on an n x n grid ★★
Author(s): Erickson
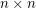 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15. Keywords: game
Outward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; outward reloid; reloid
Covering a square with unit squares ★★
Author(s):
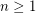 , it is impossible to cover a square of side greater than
, it is impossible to cover a square of side greater than  with
with 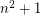 unit squares.
unit squares. Keywords:
Reloid corresponding to funcoid is between outward and inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; outward reloid; reloid
Monovalued reloid and its restrictions ★★
Author(s): Porton
Keywords: monovalued morphism; monovalued reloid; reloid
Intersection of complete funcoids ★★
Author(s): Porton
 ,
,  are complete funcoids (generalized closures) then
are complete funcoids (generalized closures) then 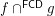 is a complete funcoid (generalized closure).
is a complete funcoid (generalized closure). Keywords: complete funcoid; funcoid; generalized closure
The Berge-Fulkerson conjecture ★★★★
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 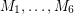 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 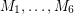 .
.
Keywords: cubic; perfect matching
Monovalued reloid is a restricted function ★★
Author(s): Porton
Keywords: monovalued morphism; monovalued reloid; reloid

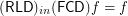 for any
for any 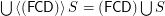 if
if 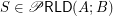 is a set of
is a set of  to a set
to a set  .
. 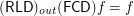 for any
for any ![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
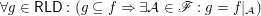 .
. 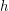 are
are 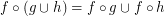 ; \item
; \item 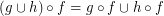 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University