 login/create account
login/create account
Covering a square with unit squares
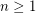 , it is impossible to cover a square of side greater than
, it is impossible to cover a square of side greater than  with
with 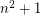 unit squares.
unit squares. Alexander Soifer in [S] raises the question of the smallest number 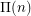 of unit squares that can cover a square of side
of unit squares that can cover a square of side  . He shows the asymptotic upper bound
. He shows the asymptotic upper bound 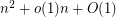 , and the small values
, and the small values 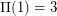 ,
, 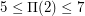 , and
, and 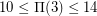 . He conjectures the asymptotic lower bound
. He conjectures the asymptotic lower bound 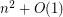 .
.
Bibliography
[S] Soifer, Alexander, "Covering a square of side n+epsilon with unit squares," J. of Combinatorial Theory, Series A 113 (2006):380-383.
* indicates original appearance(s) of problem.
A flaw in the text of the conjecture
The square to cover is not a unit square.
A simple upper bound for Pi(n)
For any positive integer n: Pi(n) does not exceed sqr(n)+n+1 .
Correction
Sorry; please replace the last part by this:
Resulting upper bounds for n from 1 to 3
The given bound confirms the bounds for n=1 (3) and for n=2 (7) given by Soifer in [S] but improves the bound for n=3 (13 instead of 14).
Possibly further readings
The two articles listed below may be on the same topic but I can't get access even to the abstracts: [1] Title: A Sharper Upper Bound for Cover-Up Squared Authors: Dmytro Karabsh and Alexander Soifer Publication: Geombinatorics Quarterly Vol XVI, Issue 1, July 2006 Pages: 219 ff. (to 226 ?) [2] Title: Note on Covering Square with Equal Squares Authors: Dmytro Karabsh and Alexander Soifer Publication: Geombinatorics Quarterly Vol XVIII, Issue 1, July 2008 Pages: 13 ff. (to 17 ?)
A (currently) valid link to the referenced article
www.uccs.edu/~faculty/asoifer/docs/untitled.pdf
Correction
In the URL there has to be a tilde (ASCII code 126) between 'edu/' and 'faculty' instead of the visible blank.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
A lower bound of the upper bound from polyomino-covering in [S]
(Using instead of
instead of  )
)
In [S], Soifer derives ![$ \Pi(n) < (n-k)^2+2(k+1)[[\frac{k^2-1}{k^2+k-\sqrt{2k+2}} n]] $](/files/tex/97f11f1771afcd45f92827714150f8faa670556b.png) .
.
As he mentioned, one can improve the covering construction. Holding the square of side length 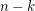 in the lower left corner, putting a square of side length
in the lower left corner, putting a square of side length  in the upper right corner, covering the remaining uncovered area by 2 polyomino-coverings of rectangles of sides
in the upper right corner, covering the remaining uncovered area by 2 polyomino-coverings of rectangles of sides 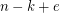 by
by 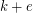 , removing useless unit squares in polyominos, we get a lower bound for the rhs of that inequality:
, removing useless unit squares in polyominos, we get a lower bound for the rhs of that inequality:
![$ (n-k)^2+k^2+2[[(k+1)(n-k)\frac{k^2-1}{k^2+k-\sqrt{2k+2}} ]] $](/files/tex/53e7346a9ad68ddeeebc33a5a499c0cd30365936.png)
Denote by 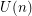 the minimal value of this expression when varying
the minimal value of this expression when varying  from 2 to
from 2 to 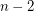 .
.
Results of computer calculations:
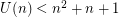 iff
iff 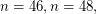 or
or 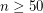 .
.
For growing  (checked up to
(checked up to 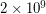 ), for the lowest optimal
), for the lowest optimal  ,
, 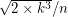 seems to converge to 1, and
seems to converge to 1, and 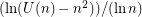 seems to converge to 3/4.
seems to converge to 3/4.