 login/create account
login/create account
Conjecture For any integer 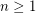 , it is impossible to cover a square of side greater than
, it is impossible to cover a square of side greater than  with
with 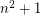 unit squares.
unit squares.
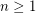 , it is impossible to cover a square of side greater than
, it is impossible to cover a square of side greater than  with
with 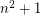 unit squares.
unit squares. Alexander Soifer in [S] raises the question of the smallest number 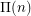 of unit squares that can cover a square of side
of unit squares that can cover a square of side  . He shows the asymptotic upper bound
. He shows the asymptotic upper bound 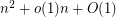 , and the small values
, and the small values 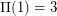 ,
, 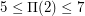 , and
, and 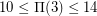 . He conjectures the asymptotic lower bound
. He conjectures the asymptotic lower bound 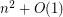 .
.
Bibliography
[S] Soifer, Alexander, "Covering a square of side n+epsilon with unit squares," J. of Combinatorial Theory, Series A 113 (2006):380-383.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University