Home » Subject » Theoretical Comp. Sci. » Complexity » Hardness of Approximation
Importance: High ✭✭✭
Author(s): Feige, Uriel
Subject: Theoretical Computer Science
» Complexity
» » Hardness of Approximation
Keywords: NP
randomness in TCS
satisfiability
Recomm. for undergrads: no
Posted by: cwenner
on: February 27th, 2009
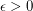Conjecture   For every rational $ \epsilon > 0 $ and every rational $ \Delta $, there is no polynomial-time algorithm for the following problem.

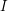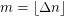Given is a 3SAT (3CNF) formula $ I $ on $ n $ variables, for some $ n $, and $ m = \floor{\Delta n} $ clauses drawn uniformly at random from the set of formulas on $ n $ variables. Return with probability at least 0.5 (over the instances) that 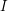$ I $ is typical without returning typical for any instance with at least 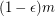$ (1 - \epsilon)m $ simultaneously satisfiable clauses.

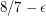This conjecture was presented in Average Case Complexity and Approximation Complexity by Uriel Feige as a new approach for showing inapproximabiltiy results $ ^\text{[F02]} $. The conjecture is strong in that it immediately implies the optimal $ 8/7 - \epsilon $-hardness of approximation of 3SAT, something shown NP-hard in 1997 with heavy applications of PCP-techniques $ ^\text{[H97]} $.

The strong and weak form

The weak form of Feige's conjecture is implied by the strong form of the conjecture (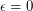$ \epsilon = 0 $) and therefore subjectively more likely to be true. In the weak form, the choice of ambiguities of the uniform distribution (such as choosing clauses with or without replacement) may affect the parameters of the conjecture but not the truth.

Support for and against the conjecture

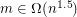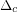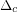If the number of clauses is large enough ($ m \in \Omega(n^{1.5}) $), then the problem defined above can be solved in polynomial time $ ^\text{[FO06]} $. 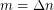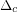It is believed that there is a phase transition $ \Delta_c $ in the probability of satisfying a random 3SAT instance such that for every $ \Delta $ sufficiently smaller than $ \Delta_c $, only an inverse exponential number of 3SAT instances with $ m = \Delta n $ clauses are not satisfiable; and for every $ \Delta $ sufficiently larger than $ \Delta_c $, only an inverse exponential number of 3SAT instances with 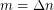$ m = \Delta n $ clauses are satisfiable. Around 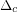$ \Delta_c $, it is also believed that deciding satisfiability of instances with about 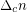$ \Delta_c n $ clauses is difficult. Feige's conjecture plausibly implies the conjecture about the hardness around 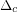$ \Delta_c $, even if 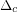$ \Delta_c $ depends on $ n $. 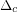The converse does not necessarily hold, that is, hardness of deciding 3SAT at $ \Delta_c $ implying hardness of the above problem for every $ \Delta $ $ ^\text{[F99]} $. (expand this section)

Value of the conjecture

By assuming that this conjecture holds, a number of inapproximability results have been derived for problems that have so far resisted attacks by other conjectures and techniques such as the unique games conjecture and probabilistically checkable proofs. If approximating a problem within 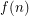$ f(n) $ implies that Feige's conjecture is false, then the problem is said to be R3SAT-hard to approximate within 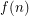$ f(n) $. It has been shown that it is R3SAT-hard to approximate Maximum Balanced Bipartite Clique for some 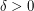$ \delta > 0 $ within 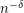$ n^{-\delta} $, Minimum Bisection below 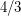$ 4/3 $, Dense k-Subgraph within some constant greater than 1, and the 2-Catalog Problem below some constant greater than 1. Showing either of these results without assuming the conjecture (e.g. NP-hardness) or improving the results assuming the conjecture are also open problems (of supposed medium importance for good enough improvements).

A result proving the problem defined in the conjecture true under more plausible conjectures, e.g. P 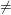$ \neq $ NP, might show the way for a host of similar results (e.g. further reductions and similar extensions for other classes), add another technique to our repertoire, and greatly expand the area studying the relation between average-case hardness and approximability hardness.

Using so-called quasi-random PCPs, Subhash Khot has shown that neither of the three above problems admit a PTAS under the assumption that 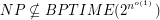$ NP \nsubseteq BPTIME(2^{n^{o(1)}}) $ $ ^\text{[K04]} $.

Related Problems

- The phase transition of random 3SAT instances (high importance) $ ^\text{[F99]} $.

- Alakhnovich's conjectures about hardness of linear systems and code words (medium importance) $ ^\text{[A03]} $.

Bibliography

[A03] Michael Alakhnovich. More on average case vs approximation complexity. FOCS 2003. http://www.math.ias.edu/~misha/papers/average.ps

*[F02] Uriel Feige. Relations between Average Case Complexity and Approximation Complexity. STOC 2002. http://citeseer.ist.psu.edu/old/feige02relations.html

[F99] Ehud Friedgut. Necessary and sufficient conditions for sharp thresholds of graph properties and the $ k $-SAT problem. Journal of the Amercian Mathematical Society, 1999.

[FO06] Uriel Feige, Eran Ofek. Easily refutable subformulas of large random 3CNF formulas. Theory of Comuting, Volume 3 (2007). Pages 25 through 43.

[H97] Johan Håstad. Some optimal inapproximability results. STOC, Proceedings of the 29th Annual ACM Symposium on Theory of Computing, 1997. http://www.nada.kth.se/~johanh/optimalinap.ps

[K04] Subhash Khot. Ruling Out PTAS for Graph Min-Bisection, Densest Subgraph and Bipartite Clique. FOCS, Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, 2004. http://www.cc.gatech.edu/~khot/papers/mdc-bc.ps


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options