Home » Subject » Topology
Importance: Outstanding ✭✭✭✭
Author(s): Smale, S.
Subject: Topology
Keywords: 4-sphere
diffeomorphisms
Recomm. for undergrads: no
Posted by: rybu
on: November 7th, 2009
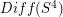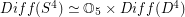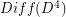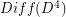Problem   $ Diff(S^4) $ has the homotopy-type of a product space $ Diff(S^4) \simeq \mathbb O_5 \times Diff(D^4) $ where $ Diff(D^4) $ is the group of diffeomorphisms of the 4-ball which restrict to the identity on the boundary. Determine some (any?) homotopy or homology groups of $ Diff(D^4) $.

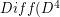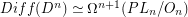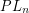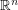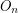$ Diff(D^4 $) is known to be a $ 5 $-fold loop space. In particular there is a homotopy-equivalence known as the Cerf-Morlet Comparison theorem $ Diff(D^n) \simeq \Omega^{n+1} (PL_n / O_n) $ where $ PL_n $ is the group of PL-automorphisms of $ \mathbb R^n $ and $ O_n $ is the group of linear automorphisms of 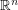$ \mathbb R^n $. Otherwise there is not much in the literature about 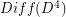$ Diff(D^4) $. Since it is a group of diffeomorphisms it has the homotopy type of a countable CW-complex. It is unknown whether or not it is connected, or if it has any other non-trivial homotopy or homology groups.

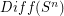$ Diff(S^n) $ is known to have the homotopy-type of 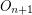$ O_{n+1} $ provided 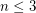$ n \leq 3 $ by work of Hatcher and Smale respectively. For 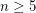$ n \geq 5 $ many of the groups 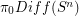$ \pi_0 Diff(S^n) $ were computed by Kervaire and Milnor, who further related these groups to the homotopy groups of spheres. For 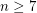$ n \geq 7 $ the rational homotopy groups of 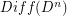$ Diff(D^n) $ have been computed by Farrell and Hsiang in range 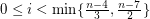$ 0 \leq i < \min\{\frac{n-4}{3}, \frac{n-7}{2} \} $. They show $ \pi_i Diff(D^n) \otimes \mathbb Q \simeq \left\{ \begin{array}{lr} \mathbb Q & \text{ provided }\ 4 | (i+1) <br> 0 & \text{ otherwise } \end{array} \right. $.

Related problems

Smooth 4-dimensional Schoenflies problem

Bibliography

[B] Budney, R. Little cubes and long knots. Topology. 46 (2007) 1--27.

[FH] Farrell, F.T. Hsiang, W.C. On the rational homotopy groups of the diffeomorphism groups of discs, spheres and aspherical manifolds. Proc. Symp. Pure. Math. 32 (1977) 403--415.

[H] Hatcher, A proof of a Smale conjecture, 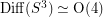$ {\rm Diff}(S\sp{3})\simeq {\rm O}(4) $. Ann. of Math. (2) 117 (1983), no. 3, 553--607.

[KS] Kirby, R. Siebenmann, L. Foundational Essays on Topological Manifolds, Smoothings, and Triangulations. Princeton University Press.

*[S] Smale, S. Diffeomorphisms of the 2-sphere, Proc. Amer. Math. Soc. 10 (1959) 621--626.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options