 login/create account
login/create account
Number of Cliques in Minor-Closed Classes ★★
Author(s): Wood
 such that every
such that every  -vertex
-vertex 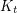 -minor-free graph has at most
-minor-free graph has at most 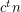 cliques?
cliques? A gold-grabbing game ★★
Author(s): Rosenfeld
Setup Fix a tree  and for every vertex
and for every vertex 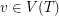 a non-negative integer
a non-negative integer 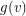 which we think of as the amount of gold at
which we think of as the amount of gold at  .
.
2-Player game Players alternate turns. On each turn, a player chooses a leaf vertex  of the tree, takes the gold at this vertex, and then deletes
of the tree, takes the gold at this vertex, and then deletes  . The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
. The game ends when the tree is empty, and the winner is the player who has accumulated the most gold.
Crossing numbers and coloring ★★★
Author(s): Albertson
We let 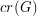 denote the crossing number of a graph
denote the crossing number of a graph  .
.
 with
with 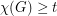 satisfies
satisfies 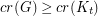 .
. Keywords: coloring; complete graph; crossing number
Domination in cubic graphs ★★
Author(s): Reed
 satisfy
satisfy 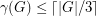 ?
? Keywords: cubic graph; domination
Do filters complementive to a given filter form a complete lattice? ★★
Author(s): Porton
Let 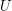 is a set. A filter (on
is a set. A filter (on 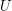 )
) 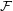 is by definition a non-empty set of subsets of
is by definition a non-empty set of subsets of 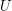 such that
such that 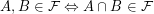 . Note that unlike some other authors I do not require
. Note that unlike some other authors I do not require 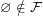 . I will denote
. I will denote 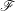 the lattice of all filters (on
the lattice of all filters (on 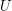 ) ordered by set inclusion.
) ordered by set inclusion.
Let 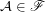 is some (fixed) filter. Let
is some (fixed) filter. Let 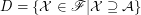 . Obviously
. Obviously  is a bounded lattice.
is a bounded lattice.
I will call complementive such filters 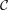 that:
that:
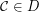 ;
;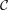 is a complemented element of the lattice
is a complemented element of the lattice  .
.
Keywords: complete lattice; filter

 Drupal
Drupal CSI of Charles University
CSI of Charles University