 login/create account
login/create account
We let 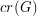 denote the crossing number of a graph
denote the crossing number of a graph  .
.
Conjecture Every graph  with
with 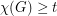 satisfies
satisfies 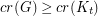 .
.
 with
with 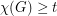 satisfies
satisfies 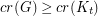 .
. This conjecture is an interesting weakening of the disproved Hajos Conjecture which asserted that 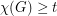 implies that
implies that  contains a subdivision of
contains a subdivision of 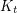 .
.
A minimal counterexample to Albertson's conjecture is critical, with minimum degree 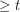 . Using this and the crossing lemma, Albertson, Cranston and Fox showed that a minimum counterexample has at most
. Using this and the crossing lemma, Albertson, Cranston and Fox showed that a minimum counterexample has at most 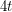 vertices. They then analyzed small cases to show that the conjecture holds for
vertices. They then analyzed small cases to show that the conjecture holds for 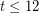 . More recently, Barat and Toth [BT] sharpened these arguments to show that the conjecture holds for
. More recently, Barat and Toth [BT] sharpened these arguments to show that the conjecture holds for 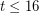 .
.
Bibliography
[BT] J. Barat and G. Toth, Towards the Albertson Conjecture
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University