 login/create account
login/create account
Distribution and upper bound of mimic numbers ★★
Author(s): Bhattacharyya
Problem
Let the notation 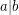 denote ''
denote '' divides
divides  ''. The mimic function in number theory is defined as follows [1].
''. The mimic function in number theory is defined as follows [1].
Definition For any positive integer 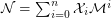 divisible by
divisible by 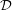 , the mimic function,
, the mimic function, 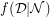 , is given by,
, is given by,
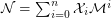 divisible by
divisible by 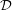 , the mimic function,
, the mimic function, 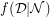 , is given by,
, is given by,
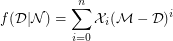
By using this definition of mimic function, the mimic number of any non-prime integer is defined as follows [1].
Definition The number  is defined to be the mimic number of any positive integer
is defined to be the mimic number of any positive integer 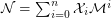 , with respect to
, with respect to 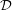 , for the minimum value of which
, for the minimum value of which 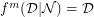 .
.
 is defined to be the mimic number of any positive integer
is defined to be the mimic number of any positive integer 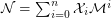 , with respect to
, with respect to 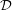 , for the minimum value of which
, for the minimum value of which 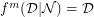 .
. Given these two definitions and a positive integer 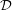 , find the distribution of mimic numbers of those numbers divisible by
, find the distribution of mimic numbers of those numbers divisible by 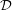 .
.
Again, find whether there is an upper bound of mimic numbers for a set of numbers divisible by any fixed positive integer 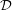 .
.
Keywords: Divisibility; mimic function; mimic number
Twin prime conjecture ★★★★
Author(s):
Conjecture There exist infinitely many positive integers  so that both
so that both  and
and 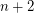 are prime.
are prime.
 so that both
so that both  and
and 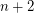 are prime.
are prime.
Keywords: prime; twin prime

 Drupal
Drupal CSI of Charles University
CSI of Charles University