 login/create account
login/create account
Are different notions of the crossing number the same? ★★★
 ?
? ![\[ \text{pair-cr}(G) = \text{cr}(G) \]](/files/tex/8cece1e00bb0e9fc122e0a5cad0dab2681cf33a4.png)
The crossing number 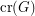 of a graph
of a graph  is the minimum number of edge crossings in any drawing of
is the minimum number of edge crossings in any drawing of  in the plane. In the pairwise crossing number
in the plane. In the pairwise crossing number 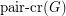 , we minimize the number of pairs of edges that cross.
, we minimize the number of pairs of edges that cross.
Keywords: crossing number; pair-crossing number
Shuffle-Exchange Conjecture (graph-theoretic form) ★★★
Author(s): Beneš; Folklore; Stone
Given integers 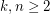 , the 2-stage Shuffle-Exchange graph/network, denoted
, the 2-stage Shuffle-Exchange graph/network, denoted 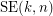 , is the simple
, is the simple  -regular bipartite graph with the ordered pair
-regular bipartite graph with the ordered pair 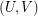 of linearly labeled parts
of linearly labeled parts 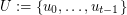 and
and 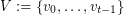 , where
, where 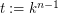 , such that vertices
, such that vertices 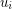 and
and 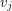 are adjacent if and only if
are adjacent if and only if  (see Fig.1).
(see Fig.1).
Given integers 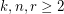 , the
, the  -stage Shuffle-Exchange graph/network, denoted
-stage Shuffle-Exchange graph/network, denoted 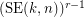 , is the proper (i.e., respecting all the orders) concatenation of
, is the proper (i.e., respecting all the orders) concatenation of 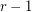 identical copies of
identical copies of 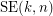 (see Fig.1).
(see Fig.1).
Let 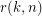 be the smallest integer
be the smallest integer 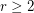 such that the graph
such that the graph 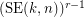 is rearrangeable.
is rearrangeable.
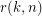 .
. 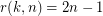 .
. Keywords:
Partition of Complete Geometric Graph into Plane Trees ★★
Author(s):
Keywords: complete geometric graph, edge colouring
Edge-Colouring Geometric Complete Graphs ★★
Author(s): Hurtado
 vertices has an edge colouring such that:
vertices has an edge colouring such that:- \item[Variant A] crossing edges get distinct colours, \item[Variant B] disjoint edges get distinct colours, \item[Variant C] non-disjoint edges get distinct colours, \item[Variant D] non-crossing edges get distinct colours.
Keywords: geometric complete graph, colouring

 Drupal
Drupal CSI of Charles University
CSI of Charles University