Home » Subject » Geometry
Importance: Medium ✭✭
Author(s): Hurtado, Ferran
Subject: Geometry
Keywords: geometric complete graph, colouring
Recomm. for undergrads: yes
Posted by: David Wood
on: October 19th, 2009
Question   What is the minimum number of colours such that every complete geometric graph on $ n $ vertices has an edge colouring such that:
    \item[Variant A] crossing edges get distinct colours, \item[Variant B] disjoint edges get distinct colours, \item[Variant C] non-disjoint edges get distinct colours, \item[Variant D] non-crossing edges get distinct colours.

Let $ P $ be a set of $ n $ points in the plane with no three collinear. Draw a straight line-segment between each pair of points in $ P $. We obtain the complete geometric graph with vertex set $ P $, denoted by $ K_P $.

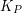Two edges in 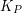$ K_P $ are either:

    \item adjacent if they have a vertex in common, \item crossing if they intersect at a point in the interior of both edges. \item disjoint if they do not intersect.

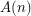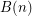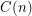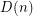Let $ A(n) $, $ B(n) $, $ C(n) $ and $ D(n) $ be the minimum number of colours for the four variants.

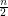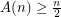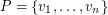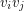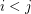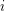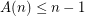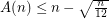Variant A: Here each colour class is a plane subgraph. Since there are point sets for which $ \frac{n}{2} $ edges are pairwise crossing, $ A(n)\geq\frac{n}{2} $. For an upper bound, say $ P=\{v_1,\dots,v_n\} $. Colour each edge $ v_iv_j $ with $ i<j $ by colour $ i $. Each colour class is a non-crossing star. So $ A(n)\leq n-1 $. Bose et al [BHRW] improved this upper bound to $ A(n)\leq n-\sqrt{\frac{n}{12}} $.

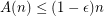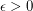Conjecture. $ A(n)\leq (1-\epsilon)n $ for some $ \epsilon>0 $.

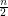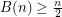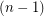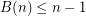Variant B: Here edges receiving the same colour must intersect. So each colour class is a geometric thrackle. Since there are point sets for which $ \frac{n}{2} $ edges are pairwise disjoint, $ B(n)\geq \frac{n}{2} $. The $ (n-1) $-colouring given in Variant A also works here. So $ B(n)\leq n-1 $.

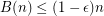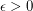Conjecture. $ B(n)\leq (1-\epsilon)n $ for some $ \epsilon>0 $.

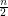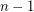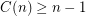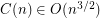Variant C: Here each colour class is a plane matching. So each colour class has at most $ \frac{n}{2} $ edges, and thus at least $ n-1 $ colours are always needed. Thus $ C(n)\geq n-1 $. Araujo [ADHNU] proved an upper bound of $ C(n)\in O(n^{3/2}) $.

Conjecture. 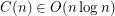$ C(n)\in O(n\log n) $.

Strong Conjecture. 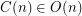$ C(n)\in O(n) $.

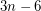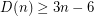Variant D: (This variant was recently mentioned in [Mat].) Here edges receiving the same colour must cross. Each colour class is called a crossing family [ADHNU]. Every edge in any triangulation of $ P $ requires its own colour. So if the convex hull of $ P $ has only three points, then at least $ 3n-6 $ colours are needed. Thus $ D(n)\geq 3n-6 $.

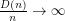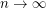Conjecture. A super-linear number of colours are always needed; i.e., $ \frac{D(n)}{n}\rightarrow\infty $ as $ n\rightarrow\infty $.

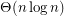A better lower bound is obtained by taking $ P $ in convex position. Then $ \Theta(n\log n) $ is the minimum number of colours [KK]. I am not aware of any non-trivial upper bound for arbitrary point sets $ P $.

Bibliography

[ADHNU] G. Araujo, A. Dumitrescu, F. Hurtado, M. Noy, J. Urrutia, On the chromatic number of some geometric type Kneser graphs, Computational Geometry: Theory & Applications 32(1):59–69, 2005 MathSciNet

[BHRW] Prosenjit Bose, Ferran Hurtado, Eduardo Rivera-Campo, David R. Wood. Partitions of complete geometric graphs into plane trees, Computational Geometry: Theory & Applications 34(2):116-125, 2006. MathSciNet

[AEGKKPS] B. Aronov, P. Erdos, W. Goddard, D.J. Kleitman, M. Klugerman, J. Pach, L.J. Schulman, Crossing families, Combinatorica 14(2):127–134, 1994. MathSciNet

[KK] Alexandr Kostochka and Jan Kratochvil. Covering and coloring polygon-circle graphs, Discrete Math. 163(1--3):299--305, 1997. MathSciNet

[Mat] Jiří Matoušek. Blocking visibility for points in general position. Discrete Comput. Geom. 42(2):219--223, 2009. MathSciNet


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options