Home » Subject » Graph Theory » Topological G.T. » Crossing numbers

Are different notions of the crossing number the same?

Importance: High ✭✭✭
Author(s): Pach, János
Tóth, Géza
Subject: Graph Theory
» Topological Graph Theory
» » Crossing numbers
Keywords: crossing number
pair-crossing number
Recomm. for undergrads: no
Posted by: cibulka
on: November 3rd, 2009
Problem   Does the following equality hold for every graph $ G $? \[ \text{pair-cr}(G) = \text{cr}(G) \]

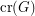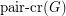The crossing number $ \text{cr}(G) $ of a graph $ G $ is the minimum number of edge crossings in any drawing of $ G $ in the plane. In the pairwise crossing number $ \text{pair-cr}(G) $, we minimize the number of pairs of edges that cross.

Obviously we have 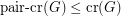$ \text{pair-cr}(G) \leq \text{cr}(G) $.

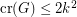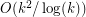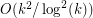The problem was first posed by Pach and Tóth in~[PT], who first spotted the possibility that the pairwise crossing number might be different from the crossing number. They proved $ \text{cr}(G) \leq 2k^2 $ for graphs with pairwise crossing number $ k $, which was later improved by Valtr~[V05] to $ O(k^2/ \log(k)) $ and by Tóth~[T08] to $ O(k^2/ \log^2(k)) $.

Bibliography

*[PT] János Pach, Géza Tóth, Which crossing number is it anyway?, Journal of Combinatorial Theory Series B 80 (2000), no. 2, 225--246. MathSciNet

[V05] Pavel Valtr, On the pair-crossing number, Combinatorial and computational geometry, 52 (2005), 569--575. MathSciNet

[T08] Géza Tóth, Note on the pair-crossing number and the odd-crossing number, Discrete Comput. Geom., 39 (2008), no. 4, 791--799. MathSciNet


* indicates original appearance(s) of problem.
add new comment