 login/create account
login/create account
Obstacle number of planar graphs ★
Author(s): Alpert; Koch; Laison
Does there exist a planar graph with obstacle number greater than 1? Is there some  such that every planar graph has obstacle number at most
such that every planar graph has obstacle number at most  ?
?
Keywords: graph drawing; obstacle number; planar graph; visibility graph
Upgrading a multifuncoid ★★
Author(s): Porton
Let 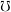 be a set,
be a set, 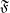 be the set of filters on
be the set of filters on 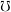 ordered reverse to set-theoretic inclusion,
ordered reverse to set-theoretic inclusion, 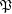 be the set of principal filters on
be the set of principal filters on 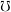 , let
, let  be an index set. Consider the filtrator
be an index set. Consider the filtrator 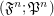 .
.
 is a multifuncoid of the form
is a multifuncoid of the form 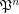 , then
, then 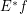 is a multifuncoid of the form
is a multifuncoid of the form 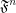 .
. See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Keywords:
Good edge labeling and girth ★★
Author(s): Bode-Farzad-Theis
More specifically: there exists a constant  such that every graph with girth at least
such that every graph with girth at least  has a good edge labeling.
has a good edge labeling.
Keywords: good edge labeling, edge labeling
Extension complexity of (convex) polygons ★★
Author(s):
The extension complexity of a polytope  is the minimum number
is the minimum number 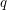 for which there exists a polytope
for which there exists a polytope 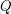 with
with 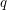 facets and an affine mapping
facets and an affine mapping  with
with 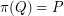 .
.
 , a convex polygon on
, a convex polygon on  vertices whose extension complexity is
vertices whose extension complexity is 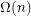 ?
? Keywords: polytope, projection, extension complexity, convex polygon
Strict inequalities for products of filters ★
Author(s): Porton
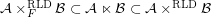 for some filter objects
for some filter objects 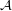 ,
, 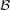 . Particularly, is this formula true for
. Particularly, is this formula true for 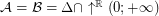 ?
? A weaker conjecture:
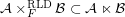 for some filter objects
for some filter objects 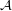 ,
, 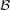 .
. Keywords: filter products

 Drupal
Drupal CSI of Charles University
CSI of Charles University