 login/create account
login/create account
Extremal problem on the number of tree endomorphism ★★
Author(s): Zhicong Lin
Conjecture An endomorphism of a graph is a mapping on the vertex set of the graph which preserves edges. Among all the  vertices' trees, the star with
vertices' trees, the star with  vertices has the most endomorphisms, while the path with
vertices has the most endomorphisms, while the path with  vertices has the least endomorphisms.
vertices has the least endomorphisms.
 vertices' trees, the star with
vertices' trees, the star with  vertices has the most endomorphisms, while the path with
vertices has the most endomorphisms, while the path with  vertices has the least endomorphisms.
vertices has the least endomorphisms. Keywords:
Which lattices occur as intervals in subgroup lattices of finite groups? ★★★★
Author(s):
Conjecture
There exists a finite lattice that is not an interval in the subgroup lattice of a finite group.
Keywords: congruence lattice; finite groups
Special Primes ★
Author(s): George BALAN
Conjecture Let  be a prime natural number. Find all primes
be a prime natural number. Find all primes 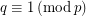 , such that
, such that 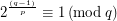 .
.
 be a prime natural number. Find all primes
be a prime natural number. Find all primes 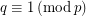 , such that
, such that 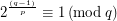 .
.
Keywords:
Hilbert-Smith conjecture ★★
Author(s): David Hilbert; Paul A. Smith
Conjecture Let  be a locally compact topological group. If
be a locally compact topological group. If  has a continuous faithful group action on an
has a continuous faithful group action on an  -manifold, then
-manifold, then  is a Lie group.
is a Lie group.
 be a locally compact topological group. If
be a locally compact topological group. If  has a continuous faithful group action on an
has a continuous faithful group action on an  -manifold, then
-manifold, then  is a Lie group.
is a Lie group. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University