 login/create account
login/create account
Characterization of monovalued reloids with atomic domains ★★
Author(s): Porton
Conjecture Every monovalued reloid with atomic domain is either
- an injective reloid;
- a restriction of a constant function
(or both).
Keywords: injective reloid; monovalued reloid
Composition of reloids expressed through atomic reloids ★★
Author(s): Porton
Conjecture If  and
and 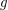 are composable reloids, then
are composable reloids, then 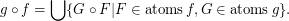
 and
and 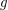 are composable reloids, then
are composable reloids, then 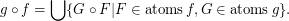
Keywords: atomic reloids
Lindelöf hypothesis ★★
Author(s): Lindelöf
Conjecture For any 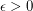
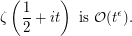
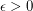
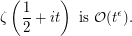
Since  can be replaced by a smaller value, we can also write the conjecture as, for any positive
can be replaced by a smaller value, we can also write the conjecture as, for any positive  ,
, 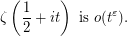
Keywords: Riemann Hypothesis; zeta
Outer reloid of direct product of filters ★★
Author(s): Porton
Question 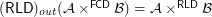 for every f.o.
for every f.o. 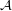 ,
, 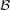 ?
?
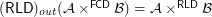 for every f.o.
for every f.o. 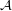 ,
, 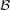 ?
? Keywords: direct product of filters; outer reloid

 Drupal
Drupal CSI of Charles University
CSI of Charles University