Home » Subject » Topology
Importance: Medium ✭✭
Author(s): Porton, Victor
Subject: Topology
Keywords: atomic reloids
Recomm. for undergrads: no
Posted by: porton
on: October 26th, 2010
Solved by: Porton, Victor
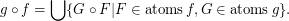
Conjecture   If $ f $ and $ g $ are composable reloids, then $$g \circ f = \bigcup \{G \circ F | F \in \mathrm{atoms}\, f, G \in \mathrm{atoms}\, g \}.$$

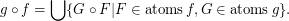
See Algebraic General Topology for definitions of used concepts.

In the same book there is a proof.

Bibliography

*Victor Porton. Algebraic General Topology


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options