 login/create account
login/create account
Join of oblique products ★★
Author(s): Porton
Conjecture 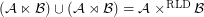 for every filter objects
for every filter objects 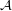 ,
, 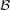 .
.
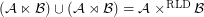 for every filter objects
for every filter objects 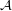 ,
, 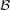 .
. Keywords: filter; oblique product; reloidal product
Author(s): Porton
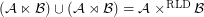 for every filter objects
for every filter objects 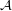 ,
, 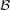 .
. Keywords: filter; oblique product; reloidal product