 login/create account
login/create account
Forcing a $K_6$-minor ★★
Author(s): Barát ; Joret; Wood
Conjecture Every graph with minimum degree at least 7 contains a 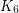 -minor.
-minor.
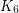 -minor.
-minor. Conjecture Every 7-connected graph contains a 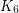 -minor.
-minor.
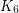 -minor.
-minor. Keywords: connectivity; graph minors
Funcoidal products inside an inward reloid ★★
Author(s): Porton
Conjecture (solved) If 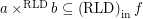 then
then 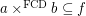 for every funcoid
for every funcoid  and atomic f.o.
and atomic f.o.  and
and  on the source and destination of
on the source and destination of  correspondingly.
correspondingly.
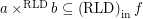 then
then 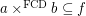 for every funcoid
for every funcoid  and atomic f.o.
and atomic f.o.  and
and  on the source and destination of
on the source and destination of  correspondingly.
correspondingly. A stronger conjecture:
Conjecture If 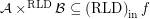 then
then 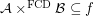 for every funcoid
for every funcoid  and
and 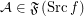 ,
, 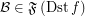 .
.
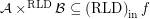 then
then 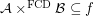 for every funcoid
for every funcoid  and
and 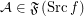 ,
, 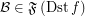 .
. Keywords: inward reloid
Distributivity of inward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; inward reloid; reloid

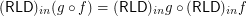 for any composable
for any composable 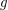 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University