 login/create account
login/create account
Special Primes
Conjecture Let  be a prime natural number. Find all primes
be a prime natural number. Find all primes 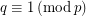 , such that
, such that 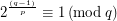 .
.
 be a prime natural number. Find all primes
be a prime natural number. Find all primes 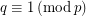 , such that
, such that 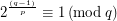 .
.
Bibliography
* indicates original appearance(s) of problem.
paul newell
On February 17th, 2012 Anonymous says:
q divides 2^((q-1)/P))-1 iff p divides (q-1)/( Order of2 mod q )

 Drupal
Drupal CSI of Charles University
CSI of Charles University
All primes are
All primes are p=(q-1)/(order of 2 mod q)