 login/create account
login/create account
Do any three longest paths in a connected graph have a vertex in common? ★★
Author(s): Gallai
Conjecture Do any three longest paths in a connected graph have a vertex in common?
Keywords:
Coloring the union of degenerate graphs ★★
Author(s): Tarsi
Conjecture The union of a 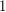 -degenerate graph (a forest) and a
-degenerate graph (a forest) and a  -degenerate graph is
-degenerate graph is  -colourable.
-colourable.
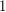 -degenerate graph (a forest) and a
-degenerate graph (a forest) and a  -degenerate graph is
-degenerate graph is  -colourable.
-colourable. Keywords:
Arc-disjoint strongly connected spanning subdigraphs ★★
Author(s): Bang-Jensen; Yeo
Conjecture There exists an ineteger  so that every
so that every  -arc-connected digraph contains a pair of arc-disjoint strongly connected spanning subdigraphs?
-arc-connected digraph contains a pair of arc-disjoint strongly connected spanning subdigraphs?
 so that every
so that every  -arc-connected digraph contains a pair of arc-disjoint strongly connected spanning subdigraphs?
-arc-connected digraph contains a pair of arc-disjoint strongly connected spanning subdigraphs? Keywords:
Arc-disjoint out-branching and in-branching ★★
Author(s): Thomassen
Conjecture There exists an integer  such that every
such that every  -arc-strong digraph
-arc-strong digraph  with specified vertices
with specified vertices  and
and  contains an out-branching rooted at
contains an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint.
which are arc-disjoint.
 such that every
such that every  -arc-strong digraph
-arc-strong digraph  with specified vertices
with specified vertices  and
and  contains an out-branching rooted at
contains an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint.
which are arc-disjoint.
Keywords:
Strong edge colouring conjecture ★★
A strong edge-colouring of a graph  is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index
is a edge-colouring in which every colour class is an induced matching; that is, any two vertices belonging to distinct edges with the same colour are not adjacent. The strong chromatic index 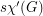 is the minimum number of colours in a strong edge-colouring of
is the minimum number of colours in a strong edge-colouring of  .
.
Conjecture 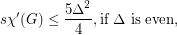
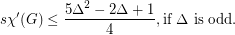
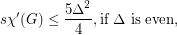
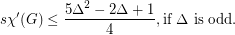
Keywords:
Long directed cycles in diregular digraphs ★★★
Author(s): Jackson
Conjecture Every strong oriented graph in which each vertex has indegree and outdegree at least  contains a directed cycle of length at least
contains a directed cycle of length at least 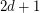 .
.
 contains a directed cycle of length at least
contains a directed cycle of length at least 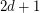 .
. Keywords:
Splitting a digraph with minimum outdegree constraints ★★★
Author(s): Alon
Problem Is there a minimum integer 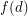 such that the vertices of any digraph with minimum outdegree
such that the vertices of any digraph with minimum outdegree  can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least
can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least  ?
?
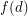 such that the vertices of any digraph with minimum outdegree
such that the vertices of any digraph with minimum outdegree  can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least
can be partitioned into two classes so that the minimum outdegree of the subgraph induced by each class is at least  ?
? Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University