 login/create account
login/create account
Long directed cycles in diregular digraphs
Conjecture Every strong oriented graph in which each vertex has indegree and outdegree at least  contains a directed cycle of length at least
contains a directed cycle of length at least 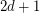 .
.
 contains a directed cycle of length at least
contains a directed cycle of length at least 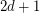 .
. The disjoint union of two regular tournaments on 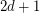 vertices shows that this would be best possible.
vertices shows that this would be best possible.
If the oriented graph has order at most 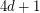 , Jackson conjecture the existence of a longer cycle, namely a Hamilton cycle
, Jackson conjecture the existence of a longer cycle, namely a Hamilton cycle
Bibliography
*[J] B. Jackson. Long paths and cycles in oriented graphs. J. Graph Theory 5 (1981), 145--157.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University