 login/create account
login/create account
Partition of a cubic 3-connected graphs into paths of length 2. ★★
Author(s): Kelmans
Problem Does every  -connected cubic graph on
-connected cubic graph on 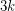 vertices admit a partition into
vertices admit a partition into  paths of length
paths of length  ?
?
 -connected cubic graph on
-connected cubic graph on 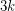 vertices admit a partition into
vertices admit a partition into  paths of length
paths of length  ?
? Keywords:
Decomposing an eulerian graph into cycles with no two consecutives edges on a prescribed eulerian tour. ★★
Author(s): Sabidussi
Conjecture Let  be an eulerian graph of minimum degree
be an eulerian graph of minimum degree 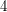 , and let
, and let 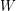 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 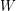 .
.
 be an eulerian graph of minimum degree
be an eulerian graph of minimum degree 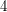 , and let
, and let 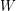 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 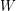 .
. Keywords:
Decomposing an eulerian graph into cycles. ★★
Author(s): Hajós
Conjecture Every simple eulerian graph on  vertices can be decomposed into at most
vertices can be decomposed into at most 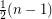 cycles.
cycles.
 vertices can be decomposed into at most
vertices can be decomposed into at most 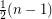 cycles.
cycles. Keywords:
Decomposing a connected graph into paths. ★★★
Author(s): Gallai
Conjecture Every simple connected graph on  vertices can be decomposed into at most
vertices can be decomposed into at most 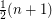 paths.
paths.
 vertices can be decomposed into at most
vertices can be decomposed into at most 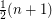 paths.
paths. Keywords:
Melnikov's valency-variety problem ★
Author(s): Melnikov
Problem The valency-variety 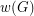 of a graph
of a graph  is the number of different degrees in
is the number of different degrees in  . Is the chromatic number of any graph
. Is the chromatic number of any graph  with at least two vertices greater than
with at least two vertices greater than 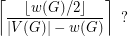
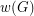 of a graph
of a graph  is the number of different degrees in
is the number of different degrees in  . Is the chromatic number of any graph
. Is the chromatic number of any graph  with at least two vertices greater than
with at least two vertices greater than 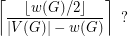
Keywords:
Do any three longest paths in a connected graph have a vertex in common? ★★
Author(s): Gallai
Conjecture Do any three longest paths in a connected graph have a vertex in common?
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University