 login/create account
login/create account
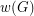 of a graph
of a graph  is the number of different degrees in
is the number of different degrees in  . Is the chromatic number of any graph
. Is the chromatic number of any graph  with at least two vertices greater than
with at least two vertices greater than 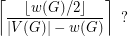
According to Jensen and Toft [JT, p. 90], the problem is due to Melnikov and was mentioned by Vizing [V] and Zykov [Z]. According to Zykov [Z], Melnikov showed that the suggested lower bound would be best possible.
A best possible upper bound on the chromatic number in terms of 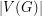 and
and 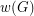 is
is 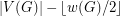 as proved by Nettleton [N] and Dirac [D].
as proved by Nettleton [N] and Dirac [D].
Bibliography
[D] G. A. Dirac. Valency-variey and chromatic number of abstract graphs. Wiss. Z. Martin-Luther-Univ. Halle-Wittenberg Math.-Natur. Reihe 13, 59--64, 1964.
[JT] Tommy R. Jensen, Bjarne Toft: Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization. John Wiley & Sons Inc., New York, 1995.
[N] R. E. Nettleton. Some generalized theorems on connectivity. Canad. J. Math. 12, 546--554, 1960.
*[V] V. G. Vizing. Some unsolved problems in graph theory (in Russian). Uspekhi Mat. Nauk. 23, 117--134, 1968. English translation in Russian Math. Surveys 23, 125--141.
*[Z] A. A. Zykov. Problem 11. In: H. Sachs, H.-J. Voss, and H. Walther, editors, Beiträge zur Graphentheorie vorgetragen auf dem Internationalen Kolloquium in Manebach DDR vom 9.-12. Mai 1967, page 228. B. G. Teubner, 1968.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University