 login/create account
login/create account
Melnikov, L. S.
Melnikov's valency-variety problem ★
Author(s): Melnikov
Problem The valency-variety 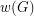 of a graph
of a graph  is the number of different degrees in
is the number of different degrees in  . Is the chromatic number of any graph
. Is the chromatic number of any graph  with at least two vertices greater than
with at least two vertices greater than 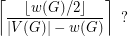
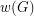 of a graph
of a graph  is the number of different degrees in
is the number of different degrees in  . Is the chromatic number of any graph
. Is the chromatic number of any graph  with at least two vertices greater than
with at least two vertices greater than 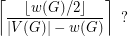
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University