 login/create account
login/create account
Hoàng-Reed Conjecture ★★★
Conjecture Every digraph in which each vertex has outdegree at least  contains
contains  directed cycles
directed cycles  such that
such that 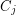 meets
meets 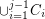 in at most one vertex,
in at most one vertex, 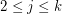 .
.
 contains
contains  directed cycles
directed cycles  such that
such that 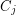 meets
meets 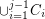 in at most one vertex,
in at most one vertex, 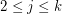 .
. Keywords:
Edge-disjoint Hamilton cycles in highly strongly connected tournaments. ★★
Author(s): Thomassen
Conjecture For every 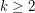 , there is an integer
, there is an integer 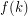 so that every strongly
so that every strongly 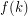 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles.
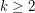 , there is an integer
, there is an integer 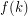 so that every strongly
so that every strongly 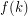 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles. Keywords:
Hamilton cycle in small d-diregular graphs ★★
Author(s): Jackson
An directed graph is  -diregular if every vertex has indegree and outdegree at least
-diregular if every vertex has indegree and outdegree at least  .
.
Conjecture For 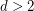 , every
, every  -diregular oriented graph on at most
-diregular oriented graph on at most 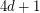 vertices has a Hamilton cycle.
vertices has a Hamilton cycle.
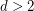 , every
, every  -diregular oriented graph on at most
-diregular oriented graph on at most 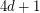 vertices has a Hamilton cycle.
vertices has a Hamilton cycle. Keywords:
Switching reconstruction of digraphs ★★
Question Are there any switching-nonreconstructible digraphs on twelve or more vertices?
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University