Decomposing a connected graph into paths.

Importance: High ✭✭✭

Author(s):

Keywords:

Recomm. for undergrads: no

Posted	by:	fhavet
	on:	March 4th, 2013

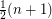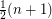Conjecture Every simple connected graph on $n$ vertices can be decomposed into at most $\frac{1}{2}(n+1)$ paths.

This conjecture is tight because a complete graph on $n$ vertices cannot be covered by less than 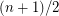$(n+1)/2$ cycles.

Bibliography

* [L] L. Lovász, On covering of graphs. In Theory of Graphs (Proc. Colloq., Tihany, 1966), 231--236. Academic Press, New York, 1968.

* indicates original appearance(s) of problem.