 login/create account
login/create account
Distributivity of a lattice of funcoids is not provable without axiom of choice ★
Author(s): Porton
Conjecture Distributivity of the lattice 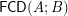 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 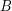 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice).
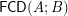 of funcoids (for arbitrary sets
of funcoids (for arbitrary sets  and
and 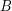 ) is not provable in ZF (without axiom of choice).
) is not provable in ZF (without axiom of choice). A similar conjecture:
Conjecture 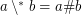 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice).
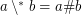 for arbitrary filters
for arbitrary filters  and
and  on a powerset cannot be proved in ZF (without axiom of choice).
on a powerset cannot be proved in ZF (without axiom of choice). Keywords: axiom of choice; distributive lattice; distributivity; funcoid; reverse math; reverse mathematics; ZF; ZFC
Almost all non-Hamiltonian 3-regular graphs are 1-connected ★★
Author(s): Haythorpe
Conjecture Denote by 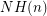 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 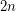 , and similarly denote by
, and similarly denote by 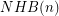 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 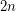 .
.
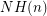 the number of non-Hamiltonian 3-regular graphs of size
the number of non-Hamiltonian 3-regular graphs of size 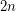 , and similarly denote by
, and similarly denote by 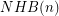 the number of non-Hamiltonian 3-regular 1-connected graphs of size
the number of non-Hamiltonian 3-regular 1-connected graphs of size 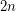 .
.
Is it true that 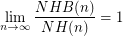 ?
?
Erdős–Faber–Lovász conjecture ★★★
Author(s): Erdos; Faber; Lovasz
Conjecture If  is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
.
 is a simple graph which is the union of
is a simple graph which is the union of  pairwise edge-disjoint complete graphs, each of which has
pairwise edge-disjoint complete graphs, each of which has  vertices, then the chromatic number of
vertices, then the chromatic number of  is
is  .
. Keywords: chromatic number
Are there only finite Fermat Primes? ★★★
Author(s):
Conjecture A Fermat prime is a Fermat number ![\[ F_n = 2^{2^n } + 1 \]](/files/tex/0da5a50010e4e5df91c0d58080245ece34ec9ca6.png) that is prime. The only known Fermat primes are F_0 =3,F_1=5,F_2=17,F_3 =257 ,F_4=65537 It is unknown if other fermat primes exist.
that is prime. The only known Fermat primes are F_0 =3,F_1=5,F_2=17,F_3 =257 ,F_4=65537 It is unknown if other fermat primes exist.
![\[ F_n = 2^{2^n } + 1 \]](/files/tex/0da5a50010e4e5df91c0d58080245ece34ec9ca6.png) that is prime. The only known Fermat primes are F_0 =3,F_1=5,F_2=17,F_3 =257 ,F_4=65537 It is unknown if other fermat primes exist.
that is prime. The only known Fermat primes are F_0 =3,F_1=5,F_2=17,F_3 =257 ,F_4=65537 It is unknown if other fermat primes exist.
Keywords:
Are all Fermat Numbers square-free? ★★★
Author(s):
Conjecture Are all Fermat Numbers ![\[ F_n = 2^{2^{n } } + 1 \]](/files/tex/70ca73d7e82af2fee084a8417e172c58cf78b376.png) Square-Free?
Square-Free?
![\[ F_n = 2^{2^{n } } + 1 \]](/files/tex/70ca73d7e82af2fee084a8417e172c58cf78b376.png) Square-Free?
Square-Free?
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University