 login/create account
login/create account
Decomposition of completions of reloids ★★
Author(s): Porton
Conjecture For composable reloids  and
and  it holds
it holds
 and
and  it holds
it holds- \item
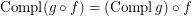 if
if  is a co-complete reloid; \item
is a co-complete reloid; \item 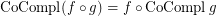 if
if  is a complete reloid; \item
is a complete reloid; \item 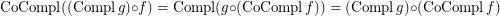 ; \item
; \item 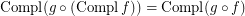 ; \item
; \item 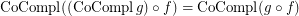 .
. Keywords: co-completion; completion; reloid
A construction of direct product in the category of continuous maps between endo-funcoids ★★★
Author(s): Porton
Consider the category of (proximally) continuous maps (entirely defined monovalued functions) between endo-funcoids.
Remind from my book that morphisms 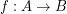 of this category are defined by the formula
of this category are defined by the formula 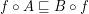 (here and below by abuse of notation I equate functions with corresponding principal funcoids).
(here and below by abuse of notation I equate functions with corresponding principal funcoids).
Let 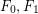 are endofuncoids,
are endofuncoids,
We define 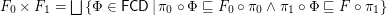
(here  and
and 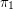 are cartesian projections).
are cartesian projections).
Conjecture The above defines categorical direct product (in the above mentioned category, with products of morphisms the same as in Set).
Keywords: categorical product; direct product
List Total Colouring Conjecture ★★
Author(s): Borodin; Kostochka; Woodall
Conjecture If  is the total graph of a multigraph, then
is the total graph of a multigraph, then 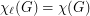 .
.
 is the total graph of a multigraph, then
is the total graph of a multigraph, then 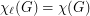 .
. Keywords: list coloring; Total coloring; total graphs
Partitioning the Projective Plane ★★
Author(s): Noel
Throughout this post, by projective plane we mean the set of all lines through the origin in 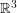 .
.
Definition Say that a subset  of the projective plane is octahedral if all lines in
of the projective plane is octahedral if all lines in  pass through the closure of two opposite faces of a regular octahedron centered at the origin.
pass through the closure of two opposite faces of a regular octahedron centered at the origin.
 of the projective plane is octahedral if all lines in
of the projective plane is octahedral if all lines in  pass through the closure of two opposite faces of a regular octahedron centered at the origin.
pass through the closure of two opposite faces of a regular octahedron centered at the origin. Definition Say that a subset  of the projective plane is weakly octahedral if every set
of the projective plane is weakly octahedral if every set 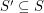 such that
such that 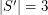 is octahedral.
is octahedral.
 of the projective plane is weakly octahedral if every set
of the projective plane is weakly octahedral if every set 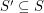 such that
such that 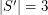 is octahedral.
is octahedral. Conjecture Suppose that the projective plane can be partitioned into four sets, say 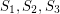 and
and 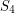 such that each set
such that each set 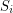 is weakly octahedral. Then each
is weakly octahedral. Then each 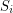 is octahedral.
is octahedral.
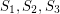 and
and 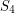 such that each set
such that each set 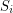 is weakly octahedral. Then each
is weakly octahedral. Then each 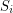 is octahedral.
is octahedral. Keywords: Partitioning; projective plane

 Drupal
Drupal CSI of Charles University
CSI of Charles University