Home » Subject » Topology
Importance: High ✭✭✭
Author(s): Porton, Victor
Subject: Topology
Keywords: categorical product
direct product
Recomm. for undergrads: no
Posted by: porton
on: August 31st, 2013
Solved by: Porton, Victor

Consider the category of (proximally) continuous maps (entirely defined monovalued functions) between endo-funcoids.

Remind from my book that morphisms 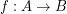$ f: A\rightarrow B $ of this category are defined by the formula 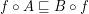$ f\circ A\sqsubseteq B\circ f $ (here and below by abuse of notation I equate functions with corresponding principal funcoids).

Let 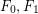$ F_0, F_1 $ are endofuncoids,

We define 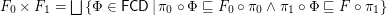$ F_0\times F_1 = \bigsqcup \left\{ \Phi \in \mathsf{FCD} \,|\, \pi_0 \circ \Phi \sqsubseteq F_0 \circ \pi_0 \wedge \pi_1 \circ \Phi \sqsubseteq F \circ \pi_1 \right\} $

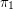(here $ \pi_0 $ and $ \pi_1 $ are cartesian projections).

Conjecture   The above defines categorical direct product (in the above mentioned category, with products of morphisms the same as in Set).

This conjecture is probably the single most important conjecture in general topology. Please help me to solve it.

Earlier I conjectured that sub-atomic product of funcoids or displaced product of funcoids are categorical direct products. But the product introduced in this blog post is (in my opinion) the most important of all different products of funcoids, the candidate for "canonical" product of funcoids.

http://www.packersandmoverschandigarh.co.in/
http://www.packersandmoversjaipur.co.in/
http://www.packersandmoversinhyderabad.co.in/
http://www.packersandmoversinbangalore.co.in/

Related problems

Sub-atomic product of funcoids is a categorical product

Bibliography

*Blog post


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options