 login/create account
login/create account
Roller Coaster permutations ★★★
Let 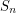 denote the set of all permutations of
denote the set of all permutations of ![$ [n]=\set{1,2,\ldots,n} $](/files/tex/470bd09059264370b76b4da90b77dc370c7e0e7c.png) . Let
. Let 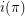 and
and 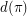 denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in
denote respectively the number of increasing and the number of decreasing sequences of contiguous numbers in  . Let
. Let 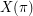 denote the set of subsequences of
denote the set of subsequences of  with length at least three. Let
with length at least three. Let 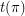 denote
denote 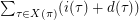 .
.
A permutation 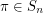 is called a Roller Coaster permutation if
is called a Roller Coaster permutation if 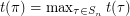 . Let
. Let 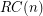 be the set of all Roller Coaster permutations in
be the set of all Roller Coaster permutations in 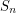 .
.
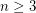 ,
,- \item If
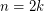 , then
, then 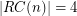 . \item If
. \item If 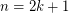 , then
, then 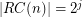 with
with 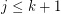 .
. 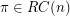 ,
,- \item If
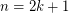 , then
, then 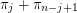 is odd for
is odd for 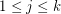 . \item If
. \item If 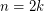 , then
, then 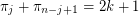 for all
for all 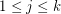 .
. Keywords:
Total Dominator Chromatic Number of a Hypercube ★★
Author(s): Adel P. Kazemi
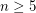 ,
, 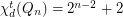 .
. Total Domination number of a hypercube ★★★
Author(s): Adel P. Kazemi
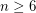 ,
, 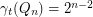 .
. Keywords: Total domination number, Hypercube
Graphs of exact colorings ★★
Author(s):
Conjecture For 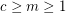 , let
, let 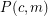 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 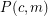 is true if and only if
is true if and only if 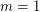 ,
, 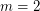 , or
, or  .
.
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University