 login/create account
login/create account
General position subsets ★★
Author(s): Gowers
Question What is the least integer 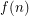 such that every set of at least
such that every set of at least 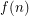 points in the plane contains
points in the plane contains  collinear points or a subset of
collinear points or a subset of  points in general position (no three collinear)?
points in general position (no three collinear)?
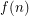 such that every set of at least
such that every set of at least 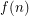 points in the plane contains
points in the plane contains  collinear points or a subset of
collinear points or a subset of  points in general position (no three collinear)?
points in general position (no three collinear)? Colouring $d$-degenerate graphs with large girth ★★
Author(s): Wood
Question Does there exist a  -degenerate graph with chromatic number
-degenerate graph with chromatic number 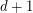 and girth
and girth  , for all
, for all 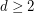 and
and 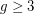 ?
?
 -degenerate graph with chromatic number
-degenerate graph with chromatic number 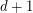 and girth
and girth  , for all
, for all 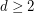 and
and 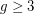 ?
? Keywords: degenerate; girth
Forcing a 2-regular minor ★★
Conjecture Every graph with average degree at least 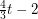 contains every 2-regular graph on
contains every 2-regular graph on  vertices as a minor.
vertices as a minor.
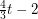 contains every 2-regular graph on
contains every 2-regular graph on  vertices as a minor.
vertices as a minor. Keywords: minors
Fractional Hadwiger ★★
Author(s): Harvey; Reed; Seymour; Wood
Conjecture For every graph  ,
,
(a)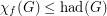
(b)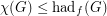
(c)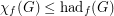 .
.
 ,
,(a)
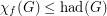
(b)
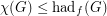
(c)
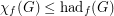 .
. Keywords: fractional coloring, minors

 Drupal
Drupal CSI of Charles University
CSI of Charles University