 login/create account
login/create account
One-way functions exist ★★★★
Author(s):
Conjecture One-way functions exist.
Keywords: one way function
Funcoid corresponding to reloid through lattice Gamma ★★
Author(s): Porton
Conjecture For every reloid  and
and 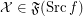 ,
, 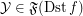 :
:
 and
and 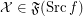 ,
, 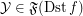 :
:- \item
![$ \mathcal{X} \mathrel{[(\mathsf{FCD}) f]} \mathcal{Y} \Leftrightarrow \forall F \in \operatorname{up}^{\Gamma (\operatorname{Src} f ; \operatorname{Dst} f)} f : \mathcal{X} \mathrel{[F]} \mathcal{Y} $](/files/tex/2f0c7dbaa1a5747d9bca753501374e8cd2500318.png) ; \item
; \item  .
. It's proved by me in this online article.
Keywords: funcoid corresponding to reloid
Restricting a reloid to lattice Gamma before converting it into a funcoid ★★
Author(s): Porton
Conjecture 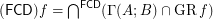 for every reloid
for every reloid 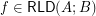 .
.
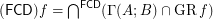 for every reloid
for every reloid 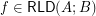 .
. Keywords: funcoid corresponding to reloid; funcoids; reloids
Inner reloid through the lattice Gamma ★★
Author(s): Porton
Conjecture 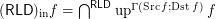 for every funcoid
for every funcoid  .
.
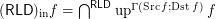 for every funcoid
for every funcoid  .
. Counter-example: 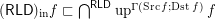 for the funcoid
for the funcoid 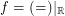 is proved in this online article.
is proved in this online article.
Keywords: filters; funcoids; inner reloid; reloids

 Drupal
Drupal CSI of Charles University
CSI of Charles University