 login/create account
login/create account
inner reloid
Inner reloid through the lattice Gamma ★★
Author(s): Porton
Conjecture 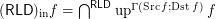 for every funcoid
for every funcoid  .
.
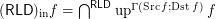 for every funcoid
for every funcoid  .
. Counter-example: 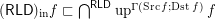 for the funcoid
for the funcoid 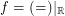 is proved in this online article.
is proved in this online article.
Keywords: filters; funcoids; inner reloid; reloids

 Drupal
Drupal CSI of Charles University
CSI of Charles University