 login/create account
login/create account
Cyclic spanning subdigraph with small cyclomatic number ★★
Author(s): Bondy
Conjecture Let  be a digraph all of whose strong components are nontrivial. Then
be a digraph all of whose strong components are nontrivial. Then  contains a cyclic spanning subdigraph with cyclomatic number at most
contains a cyclic spanning subdigraph with cyclomatic number at most 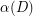 .
.
 be a digraph all of whose strong components are nontrivial. Then
be a digraph all of whose strong components are nontrivial. Then  contains a cyclic spanning subdigraph with cyclomatic number at most
contains a cyclic spanning subdigraph with cyclomatic number at most 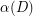 .
. Keywords:
inverse of an integer matrix ★★
Author(s): Gregory
Question I've been working on this for a long time and I'm getting nowhere. Could you help me or at least tell me where to look for help. Suppose D is an m-by-m diagonal matrix with integer elements all 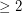 . Suppose X is an m-by-n integer matrix
. Suppose X is an m-by-n integer matrix 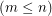 . Consider the partitioned matrix M = [D X]. Obviously M has full row rank so it has a right inverse of rational numbers. The question is, under what conditions does it have an integer right inverse? My guess, which I can't prove, is that the integers in each row need to be relatively prime.
. Consider the partitioned matrix M = [D X]. Obviously M has full row rank so it has a right inverse of rational numbers. The question is, under what conditions does it have an integer right inverse? My guess, which I can't prove, is that the integers in each row need to be relatively prime.
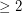 . Suppose X is an m-by-n integer matrix
. Suppose X is an m-by-n integer matrix 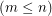 . Consider the partitioned matrix M = [D X]. Obviously M has full row rank so it has a right inverse of rational numbers. The question is, under what conditions does it have an integer right inverse? My guess, which I can't prove, is that the integers in each row need to be relatively prime.
. Consider the partitioned matrix M = [D X]. Obviously M has full row rank so it has a right inverse of rational numbers. The question is, under what conditions does it have an integer right inverse? My guess, which I can't prove, is that the integers in each row need to be relatively prime.
Keywords: invertable matrices, integer matrices

 Drupal
Drupal CSI of Charles University
CSI of Charles University