 login/create account
login/create account
Jacob Palis Conjecture(Finitude of Attractors)(Dynamical Systems) ★★★★
Author(s):
Conjecture Let 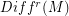 be the space of
be the space of 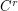 Diffeomorphisms on the connected , compact and boundaryles manifold M and
Diffeomorphisms on the connected , compact and boundaryles manifold M and 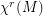 the space of
the space of 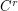 vector fields. There is a dense set
vector fields. There is a dense set 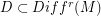 (
(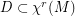 ) such that
) such that 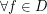 exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space
exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space 
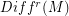 be the space of
be the space of 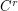 Diffeomorphisms on the connected , compact and boundaryles manifold M and
Diffeomorphisms on the connected , compact and boundaryles manifold M and 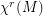 the space of
the space of 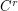 vector fields. There is a dense set
vector fields. There is a dense set 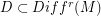 (
(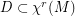 ) such that
) such that 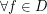 exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space
exhibit a finite number of attractor whose basins cover Lebesgue almost all ambient space 
This is a very Deep and Hard problem in Dynamical Systems . It present the dream of the dynamicist mathematicians .
Keywords: Attractors , basins, Finite
Closing Lemma for Diffeomorphism (Dynamical Systems) ★★★★
Author(s): Charles Pugh
Conjecture Let 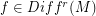 and
and 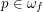 . Then for any neighborhood
. Then for any neighborhood 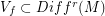 there is
there is 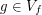 such that
such that  is periodic point of
is periodic point of 
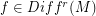 and
and 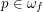 . Then for any neighborhood
. Then for any neighborhood 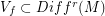 there is
there is 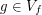 such that
such that  is periodic point of
is periodic point of 
There is an analogous conjecture for flows ( 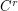 vector fields . In the case of diffeos this was proved by Charles Pugh for
vector fields . In the case of diffeos this was proved by Charles Pugh for 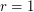 . In the case of Flows this has been solved by Sushei Hayahshy for
. In the case of Flows this has been solved by Sushei Hayahshy for 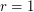 . But in the two cases the problem is wide open for
. But in the two cases the problem is wide open for 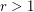
Keywords: Dynamics , Pertubation

 Drupal
Drupal CSI of Charles University
CSI of Charles University