 login/create account
login/create account
Closing Lemma for Diffeomorphism (Dynamical Systems) ★★★★
Author(s): Charles Pugh
Conjecture Let 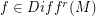 and
and 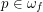 . Then for any neighborhood
. Then for any neighborhood 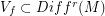 there is
there is 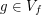 such that
such that  is periodic point of
is periodic point of 
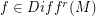 and
and 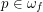 . Then for any neighborhood
. Then for any neighborhood 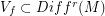 there is
there is 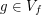 such that
such that  is periodic point of
is periodic point of 
There is an analogous conjecture for flows ( 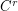 vector fields . In the case of diffeos this was proved by Charles Pugh for
vector fields . In the case of diffeos this was proved by Charles Pugh for 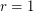 . In the case of Flows this has been solved by Sushei Hayahshy for
. In the case of Flows this has been solved by Sushei Hayahshy for 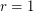 . But in the two cases the problem is wide open for
. But in the two cases the problem is wide open for 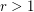
Keywords: Dynamics , Pertubation
DIS-PROOF OF BEALS CONJECTURE ★★★
Author(s):
If A(pwr)x+B(pwr)y=C(pwr)z where A,B,C,x,y,z are positive integers and x,y,z>=2,then A,B,C must have a common prime factor.
Keywords: beals conjecture
Sub-atomic product of funcoids is a categorical product ★★
Author(s):
Conjecture In the category of continuous funcoids (defined similarly to the category of topological spaces) the following is a direct categorical product:
- \item Product morphism is defined similarly to the category of topological spaces. \item Product object is the sub-atomic product. \item Projections are sub-atomic projections.
See details, exact definitions, and attempted proofs here.
Keywords:
Bounding the on-line choice number in terms of the choice number ★★
Author(s): Zhu
Question Are there graphs for which 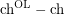 is arbitrarily large?
is arbitrarily large?
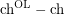 is arbitrarily large?
is arbitrarily large? Keywords: choosability; list coloring; on-line choosability

 Drupal
Drupal CSI of Charles University
CSI of Charles University