 login/create account
login/create account
A conjecture on iterated circumcentres ★★
Author(s): Goddyn
Conjecture Let 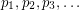 be a sequence of points in
be a sequence of points in 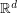 with the property that for every
with the property that for every 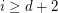 , the points
, the points 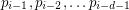 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 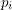 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 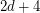 ?
?
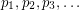 be a sequence of points in
be a sequence of points in 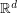 with the property that for every
with the property that for every 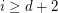 , the points
, the points 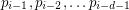 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 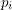 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 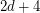 ?
? Keywords: periodic; plane geometry; sequence
The sum of the two largest eigenvalues ★★
Author(s): Gernert
Problem Let  be a graph on
be a graph on  vertices and let
vertices and let 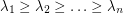 be the eigenvalues of
be the eigenvalues of  . Is
. Is 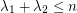 ?
?
 be a graph on
be a graph on  vertices and let
vertices and let 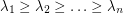 be the eigenvalues of
be the eigenvalues of  . Is
. Is 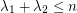 ?
? Keywords: eigenvalues; spectrum
Diagonal Ramsey numbers ★★★★
Author(s): Erdos
Let 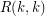 denote the
denote the 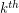 diagonal Ramsey number.
diagonal Ramsey number.
Conjecture 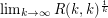 exists.
exists.
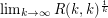 exists.
exists. Problem Determine the limit in the above conjecture (assuming it exists).
Keywords: Ramsey number
Unions of triangle free graphs ★★★
Problem Does there exist a graph with no subgraph isomorphic to 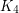 which cannot be expressed as a union of
which cannot be expressed as a union of 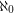 triangle free graphs?
triangle free graphs?
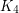 which cannot be expressed as a union of
which cannot be expressed as a union of 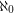 triangle free graphs?
triangle free graphs? Keywords: forbidden subgraph; infinite graph; triangle free
Half-integral flow polynomial values ★★
Author(s): Mohar
Let 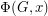 be the flow polynomial of a graph
be the flow polynomial of a graph  . So for every positive integer
. So for every positive integer  , the value
, the value 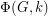 equals the number of nowhere-zero
equals the number of nowhere-zero  -flows in
-flows in  .
.
Conjecture 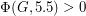 for every 2-edge-connected graph
for every 2-edge-connected graph  .
.
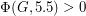 for every 2-edge-connected graph
for every 2-edge-connected graph  .
. Keywords: nowhere-zero flow

 Drupal
Drupal CSI of Charles University
CSI of Charles University