login/create account
RSS feeds
What is this? RSS is a standardized file format which is output by numerous websites including many news sites, weblogs, and the Garden. Programs called readers pick up these RSS feeds and display them.
What's the point? If there are many websites you are interested in getting information from, a reader can pick up the new information from all of them and display it for you, thus saving you the hassle of navigating everywhere to check for updates.
How do you use them? Simply choose a reader (for instance Google Reader) and then pick the websites you want to see.
Purpose
The web has become an excellent resource for locating and even learning established mathematics. Finding papers is easy with the ArXiv and MathSciNet, and (even rather technical) definitions can frequently be found on Mathworld and Wikipedia. On the other hand, the web still lacks good tools for exploration and discussion of the mathematical frontier. We hope that the Garden can help fill this void, playing a role complementary to that of these other sites. Thanks to a wonderful community of users, Wikipedia has quickly built an impressive library of established knowledge. We hope that the Garden will help our community to build an equally impressive online mapping of the frontier of our knowledge.
Open problem structure
Associated with each open problem are the following fields.
| Field | Explanation | ||||
| Title | The title used by the Garden for reference purposes. | ||||
| Statement | A consise statment of the conjecture. | ||||
| Importance |
|
is a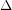 
-edge-critical graph. Suppose that for each edge 
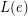of 
of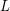 
-edge-colorable unless all lists are equal to each other. 
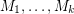are matroids on 
and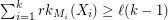 
for every partition 
of 
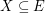with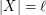 
which is independent in every 
. 
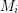Drupal
CSI of Charles University