 login/create account
login/create account
Bounding the chromatic number of graphs with no odd hole ★★★
Author(s): Gyarfas
Conjecture There exists a fixed function 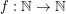 so that
so that 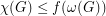 for every graph
for every graph  with no odd hole.
with no odd hole.
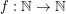 so that
so that 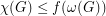 for every graph
for every graph  with no odd hole.
with no odd hole. Keywords: chi-bounded; coloring; induced subgraph; odd hole; perfect graph
Lonely runner conjecture ★★★
Conjecture Suppose  runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least
runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least  (along the track) away from every other runner.
(along the track) away from every other runner.
 runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least
runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least  (along the track) away from every other runner.
(along the track) away from every other runner. Keywords: diophantine approximation; view obstruction
Sets with distinct subset sums ★★★
Author(s): Erdos
Say that a set 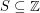 has distinct subset sums if distinct subsets of
has distinct subset sums if distinct subsets of  have distinct sums.
have distinct sums.
Conjecture There exists a fixed constant  so that
so that 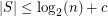 whenever
whenever 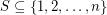 has distinct subset sums.
has distinct subset sums.
 so that
so that 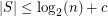 whenever
whenever 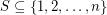 has distinct subset sums.
has distinct subset sums. Keywords: subset sum

 Drupal
Drupal CSI of Charles University
CSI of Charles University