login/create account
Conjecture Suppose 
runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least 
(along the track) away from every other runner.
runners having distinct constant speeds start at a common point and run laps on a circular track with circumference 1. Then for any given runner, there is a time at which that runner is distance at least (along the track) away from every other runner. This conjecture was independently introduced in two very different contexts. Wills [W] introduced it as a problem in diophantine approximation, and Cusick [C1] discovered it as a geometric view obstruction problem. The poetic name is due to Goddyn.
There are a number of different proofs of this conjecture for small values of (as a warning, there are different formulations of this conjecture, and what appears here as the problem for runners is sometimes considered to be the problem for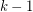 
runners). The cases with 
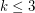runners are easy to check. The 
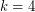case was proved independently by Betke and Wills [BW] and by Cusick. The 
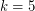case was first established by Cusick and Pomerance [CP] with the help of some computer checking, and this argument was later simplified by Bienia et al. [BGGS] who also found applications of this theorem to the study of flows on graphs. The 
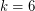case was first proved by Bohman et al. [BHK] and this was later simplified by Renault [R]. Recently, the 
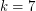case was proved by Barajas and Serra [BS].
Bibliography
[BS] J. Barajas and O. Serra, The lonely runner problem with seven runners.
[BW] U. Betke and J. M. Wills, Untere Schranken fur zwei diophantische Approximations-Funktionen, Monatsch. Math. 76 (1972), 214-217.
[BGST] W. Bienia, L. Goddyn, P. Gvozdjak, A. Sebo, Flows, View Obstructions, and the Lonely Runner, J. Combinatorial Theory Ser. B 72 (1998) 1-9.
[BHK] T. Bohman, R. Holzman, and D. Kleitman, Six lonely runners, Electron. J. Combin. 8 (2001), no. 2
[CC] Y.G. Chen, T.W. Cusick, The View-Obstruction Problem for n-Dimensional Cubes, J. Number Theory 74, no. 1 (1999) 126-133.
*[C1] T.W. Cusick, View-Obstruction Problems in n-Dimensional Geometry, J. Combinatorial Theory Ser. A 16 (1974) 1-11.
[C2] T.W. Cusick, View-Obstruction Problems II, Proc. Amer. Math. Soc. 84 (1982) 25-28.
[C3] T.W. Cusick, The view-obstruction problem for 
-dimensional cubes Monatsh. Math. 127 (1999), no. 3, 183--187.
[CP] T.W. Cusick and C. Pomerance, View-Obstruction Problems III, J. Number Theory 19 (1984) 131-139.
[R] J. Renault, View-obstruction: a shorter proof for 6 lonely runners. Discrete Math. 287 (2004), no. 1-3, 93-101.
*[W] J.M. Wills, Zwei Satze uber Inhomogene Diophantische Approximation von Irrationalzahlen, Monatsch. Math. 71 (1967) 263-269.
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University