 login/create account
login/create account
odd hole
Bounding the chromatic number of graphs with no odd hole ★★★
Author(s): Gyarfas
Conjecture There exists a fixed function 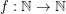 so that
so that 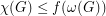 for every graph
for every graph  with no odd hole.
with no odd hole.
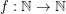 so that
so that 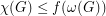 for every graph
for every graph  with no odd hole.
with no odd hole. Keywords: chi-bounded; coloring; induced subgraph; odd hole; perfect graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University