 login/create account
login/create account
The large sets conjecture ★★★
Author(s): Brown; Graham; Landman
Conjecture If 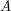 is 2-large, then
is 2-large, then 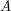 is large.
is large.
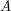 is 2-large, then
is 2-large, then 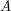 is large.
is large. Keywords: 2-large sets; large sets
Ramsey properties of Cayley graphs ★★★
Author(s): Alon
Conjecture There exists a fixed constant  so that every abelian group
so that every abelian group  has a subset
has a subset 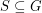 with
with 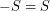 so that the Cayley graph
so that the Cayley graph 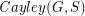 has no clique or independent set of size
has no clique or independent set of size 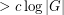 .
.
 so that every abelian group
so that every abelian group  has a subset
has a subset 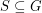 with
with 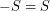 so that the Cayley graph
so that the Cayley graph 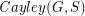 has no clique or independent set of size
has no clique or independent set of size 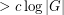 .
. Keywords: Cayley graph; Ramsey number
Bases of many weights ★★★
Let  be an (additive) abelian group, and for every
be an (additive) abelian group, and for every 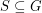 let
let 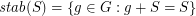 .
.
Conjecture Let 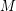 be a matroid on
be a matroid on 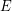 , let
, let 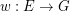 be a map, put
be a map, put 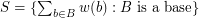 and
and 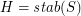 . Then
. Then 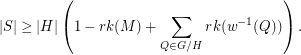
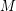 be a matroid on
be a matroid on 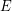 , let
, let 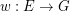 be a map, put
be a map, put 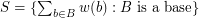 and
and 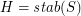 . Then
. Then 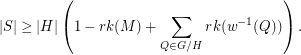

 Drupal
Drupal CSI of Charles University
CSI of Charles University