 login/create account
login/create account
Unions of triangle free graphs
Problem Does there exist a graph with no subgraph isomorphic to 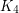 which cannot be expressed as a union of
which cannot be expressed as a union of 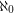 triangle free graphs?
triangle free graphs?
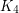 which cannot be expressed as a union of
which cannot be expressed as a union of 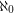 triangle free graphs?
triangle free graphs? Shelah [S] has proved that the existence of such a graph is consistent with ZFC.
Bibliography
*[EH] P. Erdos and A. Hajnal, On decomposition of graphs, Acta Math. Acad. Sci. Hungar. 18 (1967), 359–377.
[S] S. Shelah, Consistency of positive partition theorems for graphs and models, in Set Theory and Applications, Springer Lecture Notes 1401, (Toronto, ON, 1987), 167–193.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University