 login/create account
login/create account
Goldberg's conjecture ★★★
Author(s): Goldberg
The overfull parameter is defined as follows: ![\[ w(G) = \max_{H \subseteq G} \left\lceil \frac{ |E(H)| }{ \lfloor \tfrac{1}{2} |V(H)| \rfloor} \right\rceil. \]](/files/tex/d2391343543ce03d861e6eb2f4985d52e309525d.png)
Conjecture Every graph  satisfies
satisfies 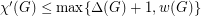 .
.
 satisfies
satisfies 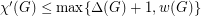 .
. Keywords: edge-coloring; multigraph
Seymour's r-graph conjecture ★★★
Author(s): Seymour
An  -graph is an
-graph is an  -regular graph
-regular graph  with the property that
with the property that 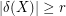 for every
for every 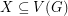 with odd size.
with odd size.
Conjecture 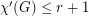 for every
for every  -graph
-graph  .
.
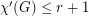 for every
for every  -graph
-graph  .
. Keywords: edge-coloring; r-graph
Discrete Logarithm Problem ★★★
Author(s):
If  is prime and
is prime and 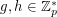 , we write
, we write 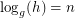 if
if 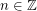 satisfies
satisfies 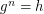 . The problem of finding such an integer
. The problem of finding such an integer  for a given
for a given 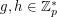 (with
(with 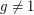 ) is the Discrete Log Problem.
) is the Discrete Log Problem.
Conjecture There does not exist a polynomial time algorithm to solve the Discrete Log Problem.
Keywords: discrete log; NP
Odd perfect numbers ★★★
Author(s): Ancient/folklore
Conjecture There is no odd perfect number.
Keywords: perfect number
Edge list coloring conjecture ★★★
Author(s):
Conjecture Let  be a loopless multigraph. Then the edge chromatic number of
be a loopless multigraph. Then the edge chromatic number of  equals the list edge chromatic number of
equals the list edge chromatic number of  .
.
 be a loopless multigraph. Then the edge chromatic number of
be a loopless multigraph. Then the edge chromatic number of  equals the list edge chromatic number of
equals the list edge chromatic number of  .
. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University