 login/create account
login/create account
Monochromatic empty triangles ★★★
Author(s):
If 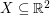 is a finite set of points which is 2-colored, an empty triangle is a set
is a finite set of points which is 2-colored, an empty triangle is a set 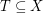 with
with 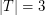 so that the convex hull of
so that the convex hull of  is disjoint from
is disjoint from  . We say that
. We say that  is monochromatic if all points in
is monochromatic if all points in  are the same color.
are the same color.
Conjecture There exists a fixed constant  with the following property. If
with the following property. If 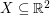 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 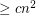 monochromatic empty triangles.
monochromatic empty triangles.
 with the following property. If
with the following property. If 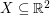 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 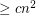 monochromatic empty triangles.
monochromatic empty triangles. Keywords: empty triangle; general position; ramsey theory
Erdös-Szekeres conjecture ★★★
Conjecture Every set of 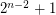 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon.
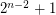 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon. Keywords: combinatorial geometry; Convex Polygons; ramsey theory
Termination of the sixth Goodstein Sequence ★
Author(s): Graham
Question How many steps does it take the sixth Goodstein sequence to terminate?
Keywords: Goodstein Sequence
Edge-antipodal colorings of cubes ★★
Author(s): Norine
We let 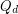 denote the
denote the  -dimensional cube graph. A map
-dimensional cube graph. A map 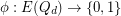 is called edge-antipodal if
is called edge-antipodal if 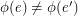 whenever
whenever 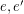 are antipodal edges.
are antipodal edges.
Conjecture If 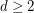 and
and 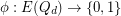 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 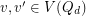 which are joined by a monochromatic path.
which are joined by a monochromatic path.
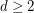 and
and 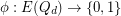 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 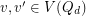 which are joined by a monochromatic path.
which are joined by a monochromatic path. Keywords: antipodal; cube; edge-coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University